Come utilizzare l’ordinamento di selezione
L’ordinamento di selezione è una tecnica di ordinamento che seleziona un elemento dell’elenco e quindi ne scambia il posto con un altro. Seleziona l’elemento più grande e poi lo scambia con un elemento nell’indice più alto dell’elenco.
L’algoritmo esegue questa operazione ripetutamente finché l’elenco non viene ordinato. Se non sei sicuro di come funziona l’ordinamento per selezione, sei nel posto giusto. Lo spiegheremo in modo più approfondito di seguito, oltre a mostrarti un esempio.
Ordinamento di selezione: uno sguardo più da vicino
Supponiamo di avere la lista: [39, 82, 2, 51, 30, 42, 7]. Per ordinare l’elenco utilizzando l’ordinamento per selezione, dovresti prima trovare il numero più alto in esso.
Con la lista data, quel numero è 82. Scambia 82 con il numero nell’indice più alto (cioè 7).
Dopo il primo passaggio, il nuovo ordine delle liste sarà: [39, 7, 2, 51, 30, 42, 82]. Ogni volta che l’algoritmo passa attraverso l’intero elenco, questo viene chiamato “pass”.
Si noti che l’elenco mantiene un sottoelenco ordinato e un sottoelenco non ordinato durante il processo di ordinamento.
L’elenco originale inizia con un elenco ordinato di zero elementi e un elenco non ordinato di tutti gli elementi. Quindi, dopo il primo passaggio, ha un elenco ordinato con solo il numero 82.
Al secondo passaggio, il numero più alto nella sottolista non ordinata sarà 51. Questo numero verrà scambiato con 42 per dare il nuovo ordine della lista di seguito:
[39, 7, 2, 42, 30, 51, 82].
Il processo viene ripetuto fino a quando non viene ordinato l’intero elenco. La figura seguente riassume l’intero processo:
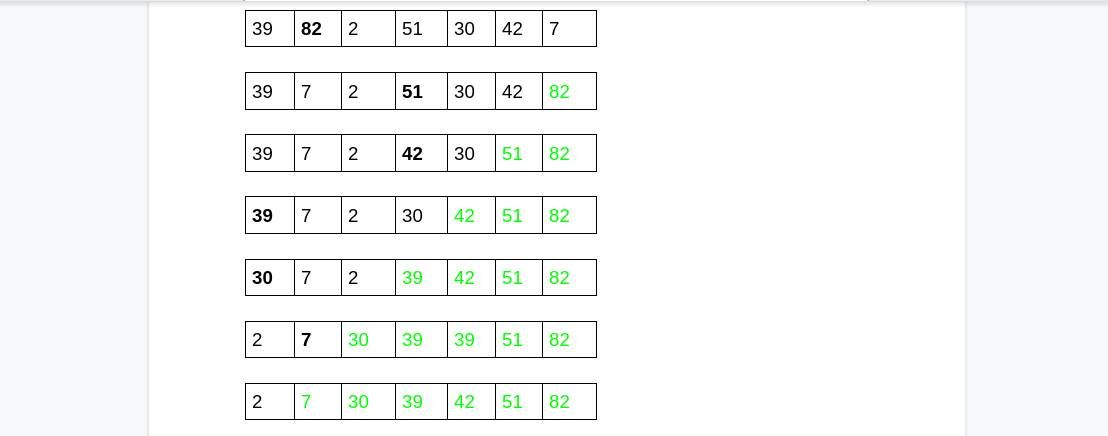
I numeri in grassetto nero mostrano il valore di elenco più alto in quel momento. Quelli in verde mostrano la sottolista ordinata.
Analisi dell’algoritmo
Per ottenere la complessità (usando la notazione Big-O) di questo algoritmo, segui di seguito:
Al primo passaggio, vengono effettuati (n-1) confronti. Al secondo passaggio, (n-2). Al terzo passaggio, (n-3) e così via fino al (n-1)esimo passaggio che fa un solo confronto.
Riassumendo i confronti come di seguito si ottiene:
(n-1)+ (n-1)+ (n-1)+…+1 = ((n-1)n)/2.
Pertanto per selezione è O (n 2).
Implementazione del codice
Il codice mostra le funzioni che è possibile utilizzare per eseguire l’ordinamento di selezione utilizzando Python e Java.
Pitone:
def selectionSort(mylist):
for x in range(len(mylist) - 1, 0, -1):
max_idx = 0
for posn in range(1, x + 1):
if mylist[posn] > mylist[max_idx]:
max_idx = posn
temp = mylist[x]
mylist[x] = mylist[max_idx]
mylist[max_idx] = tempGiava:
void selectionSort(int my_array[]){
for (int x = 0; x < my_array.length - 1; x++)
{
int index = x;
for (int y = x + 1; y < my_array.length; y++){
if (my_array[y] < my_array[index]){
index = y; // find lowest index
}
}
int temp = my_array[index]; // temp is a temporary storage
my_array[index] = my_array[x];
my_array[x] = temp;
}}Passare dall’ordinamento di selezione all’ordinamento di unione
Poiché l’analisi algoritmo di cui sopra ha dimostrato, l’algoritmo di ordinamento per selezione è O (n 2). Ha una complessità esponenziale ed è quindi inefficiente per set di dati molto grandi.
Un algoritmo molto migliore da usare sarebbe il merge sort con una complessità di O(nlogn). E ora che sai come funziona l’ordinamento di selezione, il prossimo elenco di studi per gli algoritmi di ordinamento dovrebbe essere l’ordinamento di unione.

