Introduzione all’algoritmo di ordinamento per inserimento
L’ordinamento per inserimento è una tecnica che funziona utilizzando un sottoelenco ordinato e aggiungendovi continuamente un valore dall’elenco non ordinato fino a quando non viene ordinato l’intero elenco.
L’algoritmo inizia con il primo elemento dell’elenco come sottoelenco ordinato. Quindi confronta il numero successivo con il primo. Se è maggiore, viene inserito nel primo index. Altrimenti, viene lasciato nel suo index.
Il terzo valore viene quindi confrontato con gli altri due e quindi inserito nell’indice corretto. Questo processo continua fino a quando l’intero elenco non viene ordinato.
Uno sguardo più da vicino all’ordinamento di inserimento
La descrizione sopra potrebbe non avere senso per te. Un esempio dovrebbe aiutarti a capire molto meglio.
Supponiamo di avere una lista: [39, 6, 2, 51, 30, 42, 7].
L’algoritmo identifica 39 come primo valore della sottolista ordinata. La valutazione passa poi alla seconda posizione.
6 viene poi confrontato con 39. Poiché 6 è minore di 39, 6 viene inserito nella prima posizione e 39 nella seconda. Il nuovo ordine dell’elenco è dopo il primo passaggio è ora:
[6, 39, 2, 51, 30, 42, 7]
La valutazione si sposta ora in terza posizione. 2 viene confrontato con gli ultimi due numeri e poi inserito nella giusta posizione. Il nuovo ordine dell’elenco è dopo il secondo passaggio è ora:
[2, 6, 39, 51, 30, 42, 7]
Per il terzo passaggio, l’ordine della lista è:
[2, 6, 39, 51, 30, 42, 7]
Il processo si ripete finché non viene ordinato l’intero elenco.
Vedere lo schema seguente che riassume queste operazioni:
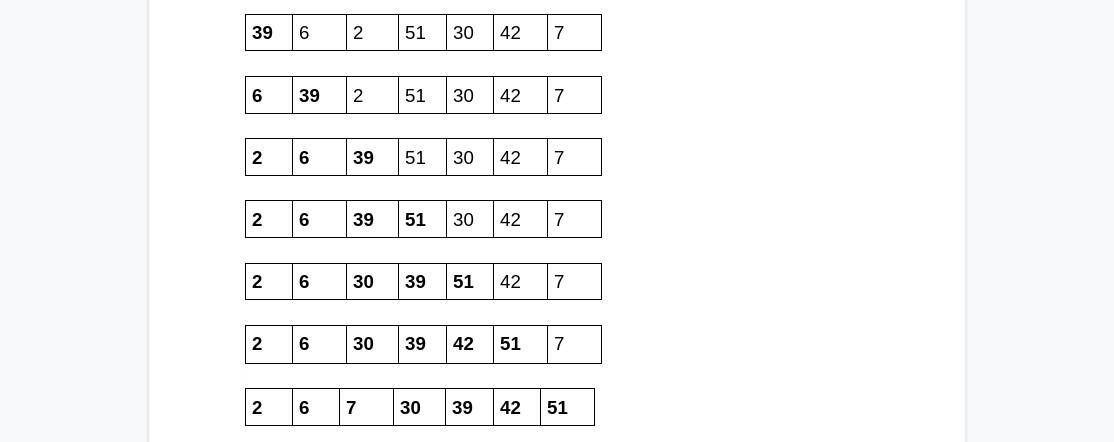
Analisi dell’algoritmo
La complessità temporale di Insertion Sort è O(n 2 ), proprio come il bubble sort . Il numero di confronti nello scenario peggiore è la somma di tutti i numeri interi da 1 a (n-1), fornendo una somma quadratica.
Implementazione del codice
Il codice Python e Java di seguito mostra come implementare il metodo Insertion Sort.
Pitone:
def insertionSort(mylist):
for step in range(1, len(mylist)):
current_element = mylist[step]
position = step
while position > 0 and mylist[position - 1] > current_element:
mylist[position] = mylist[position - 1]
position = position - 1
mylist[position] = current_elementGiava:
void insertionSort(int[] myarray) {
int n = myarray.length;
for (int x = 1; x < n; x++) {
int key = myarray[x];
int y = x-1;
while ( (y > -1) && ( myarray [y] > key ) ) {
myarray [y+1] = myarray [y];
y--;
}
myarray[y+1] = key;
}
}Migliore codifica con pseudocodice
Gli esempi di codice sopra sono stati forniti senza alcun pseudocodice a cui puoi fare riferimento per scrivere questo algoritmo in altre lingue. Alla maggior parte dei programmatori (incluso l’autore) piace correre alla tastiera dopo che gli è stato detto “sussurrando” su come funziona un programma.
Questo approccio è purtroppo soggetto a errori poiché la logica del programma diventa più complicata. Come ti piacerebbe migliorare il tuo gioco di programmazione imparando a usare lo pseudocodice?

